Bu çalışmanın konusu Oyun Teorisi’dir. Bu teorinin ortaya çıkışı uzun yıllar öncesine dayanır. Çalışmada önce oyun teorisinin tarihsel gelişimi ve uygulama alanları incelenmiştir.

İkinci bölümde, oyun teorisi ile ilgili temel kavramlar tanımlanmış, sonra oyun teorisi için başlıca önermeler verildikten sonra, diğer bölümlerde oyun teorisiyle ilgili çeşitli stratejiler ve yöntemler örneklerle desteklenerek açıklanılmaya çalışılmıştır.

1. OYUN TEORİSİ’NİN GELİŞİMİ VE UYGULAMA ALANLARI

1. Gelişimi

Samuel Johnson (1755) “oyun” kelimesini, herhangi bir şeyin eğlencesi olarak tanımlar. Modern düşünceler, bu tanıma ek olarak belirli kuralları da birleştirmiştir. Mesela, atletik oyunlardan golf, basketbol, futbol ve tenis; kart oyunlarından briç, poker; tahta oyunlarından satranç ve tavla gibi. Bu oyunlardan çoğu karşılıklı etkileşimi ve rekabeti getirir, oyuncu oyundaki diğer oyuncudan üstün olmak için çabalar ve onun başarısı, diğer oyuncuların hareketlerine ve kendi hareketlerine bağlıdır. Bu tanımlama ve örnekler oyun kelimesinin ilk algılanışı olup, gündelik hayatta kullanışına denk düşer.

Oyunun bir başka gündelik ve basit tanımlamasını Rousseau, Discourse on the Origin and Basis of Equality among Men eserinde yapmıştır:

Avcı grubu, erkek geyik avlamayı karar vermişlerse, tamamen bu amaçlarını başarmak için uğraşacaklardır. Ama eğer bir yabani tavşan onların yanından geçerse, kuşkusuz peşine düşmeye çalışmayacaktır. Gruptan biri, ilk olarak avlanırsa, arkadaşları kendinden önce avlanamadıkları için üzülecektir veya avı kaçırdıkları için biraz kaygılanacaktır.

Burada bazı boşluklar doldurulursa, sadece iki avcı olup, eş zamanlı olarak geyik mi yoksa tavşan mı avlayacaklarına karar vermelilerdir. Eğer ikisi de geyik için avlanırlarsa bir geyik yakalayıp onu eşitçe paylaşacaklar ve bir geyiği ikisi yiyeceklerdir. Eğer bir avcı geyik avlarken diğeri de tavşan için çabalarsa, biri önce geyiği diğeri de sonra tavşan yakalayacak ve her avcı, yarım geyiktense bir tavşanı (ya da tersi) tercih edecektir. Sonuçta bu basit örnek bir oyundur. Avcılar ise, oyuncudur. Her oyuncu iki strateji arasında seçim yapmak zorundadır: Geyik ya da tavşan avlamak. Seçimlerinin kaybı, bir avdır. Örneğin, geyik 4 birim fayda sağlıyorsa ve tavşanın değeri 1 ise, her iki avcı da geyik avladıklarında kayıpları 2 birim olacaktır.

İşletme ve ekonomi kaynaklarında “oyun” zamanla ortaya çıkacak olan belli ödemeleri (outcomes) önceden kestirmek için karar verme zorunluluğunda kalan tarafların (veya oyuncuların) menfaat çatışmalarını veya rekabetini yansıtır. Oyun Teorisi karmaşık yararların mücadelesini açıklayan matematiksel bir yaklaşımdır. Yararların çatışması ekonomide (sendika yöneticisi arasındaki ücret görüşmeleri oligopol piyasasındaki durumlar vb.) olağan olduğundan, son yıllarda oyun kuramına ilgi oldukça artmıştır. Hatta bazı iktisatçılar belirlenemeyen oligopolistik çözümler için başvurulabilecek en son aracın oyun kuramı modelinin olduğunu öne sürerler.

Oyun teorisi ve lineer programlama, kantitatif teknikler arasında yer alır. Aradaki ayrım oyun teorisi kavramlarıyla matrisi yazabilen oyunda seçeneklerin çok fazla olması halinde lineer programlama problemi olarak inceleme özelliğinde bulunabilir. Bununla beraber oyun teorisinde taraflar, kazançlarını mümkün olduğu kadar arttırmayı veya mümkün olduğu kadar az kaybetmeyi benimserler.

Oyun teorisi, karar teorilerinin altında incelenen bir konudur. Karar problemlerinde tek bir karar vericinin bulunduğu problemlerdir. Bu problemlerde tek bir karar verici bulunduğundan, amaç fonksiyonunun değeri, yalnızca bu karar vericinin kararına bağlı kalarak değerlendirilir. Uygulamada birden çok karar vericinin bulunduğu karar problemleriyle karşılaşmak daha olağandır. Esas amacı birbirine rakip olan ve çıkarları çatışan tarafların akılcı davranış kurallarının belirlenmesi olan oyun teorisi, bu tür karar ortamlarını açıklayan matematiksel bir yaklaşımdır.

Oyunların şans kuramı 17. Yüzyılda ortaya atılmış ve olasılık kuramı adı verilen matematik dalının gelişmesinde kaynak olmuştur. Oyun kuramına ilk değinen matematikçi Emile Barel’dir. Stratejik oyunlar kuramının bulucusu olan J. Von Neumann bu konu üzerindeki ilk çalışmasını 1928’de yayınlamıştır. Sonra Oskar Morgenstern ile birlikte “Theory of Games and Economic Behavior” adlı yapıtı 1944’de yayınlamışlardır. Bu çalışmadan sonra matematikçiler ve sosyal bilimciler, oyun kuramı ile ilgili pekçok çalışma sunmalarına karşın alanın hala araştırmaya gereksinimi vardır.

 

2. Uygulama Alanları

Oyun teorisi iş sorunlarının çözümünde yaygın olarak kullanılmamaktadır. Buna karşın rekabet unsurları içinde önemli bir görüş açıklığı sağlamıştır. Yöneticinin işi, rekabete etki eden faktörler içindeki hal tarzını göz önüne alarak, mevcut en iyi stratejiyi seçmektir. Böylece stratejinin onaylanması ve anlaşılmasında çok faydalıdır.

• Teklif verme politikalarının saptanması,
• Reklam planları,
• Satın alma politikasının belirlenmesi,
• Yeni mamuller arasından seçim yapma,
• Araştırma stratejilerinin belirlenmesi,
• Talebin belirsiz olması halinde üretim programlama,
• Fiyatlama.

1. Kavga – amaç rakibi saf dışı etmek,
2. Oyunlar – amaç zekice rakibe karşı üstün gelmek,
3. Görüşme – amaç rakibi inandırmak.

1. OYUN TEORİSİ İLE İLGİLİ TEMEL KAVRAMLAR

Oyun teorisi, karşılıklı birbirlerine bağlıyken rasyonel bireylerin nasıl karar alacaklarıyla ilgilidir. Son yıllarda bu teori ekonominin çeşitli branşlarında uygulanmaktadır. Özellikle, yeni endüstriyel ve yeni uluslararası ekonomi alanında çalışan ekonomistler faydalanırlar.

1. Oyuncular: Oyunda en az iki oyuncu veya rakip olmalı ve onların akılcı hareket ettikleri gibi kazanmak için en iyisini yaptıkları varsayılır.
2. Stratejiler: Her oyuncunun deneme seçenekleri vardır. Bir oyuncu için herhangi bir strateji kural olup, çeşitli deneme faaliyetleri arasından oyunun seçimini belirler. Herhangi bir oyuncunun deneme faaliyetleri belirsiz sayıdaysa oyun sonlu değil süreklidir. Deneme faaliyetleri belirli ise oyun sonludur. Her oyuncunun seçenek stratejisinin sayısı sonludur.
3. Kazanç veya Ödemeler: Oyunun sonucu kazanma, yitirme veya oyunsan çekilme olabilir. Her sonuç veya ödeme, negatif, pozitif veya sıfır olmak üzere her oyuncunun rakibine karşı kazancını veya kaybını belirler.
4. Ödemeler Matrisi: Bu matris, oyuncuların strateji seçimlerinin türlü bileşiminden sonuçlanan kazanç veya kayıpları gösterir. Ödeme matrisinin elemanları pozitif, negatif veya sıfıra eşit olabilir. Matrisin herhangi bir elemanı pozitif ise sütunda yer alan oyuncu, satırda yer alan oyuncuya bu miktarda ödeme yapar. Matrisin herhangi bir elemanı negatif ise satırdaki oyuncu, sütundaki oyuncuya bu negatif elemanın mutlak değerine eşit ödemede bulunur. Matrisin elemanı sıfır ise oyunculardan hiçbiri birbirine ödemede bulunmaz.
5. Oyunlar: Oyunların sınıflandırılması genellikle oyuncuların sayılarına göre yapılır. İki kişilik, üç kişilik veya (n) kişilik oyunlar kurulabilir. n=2 ise oyun 2 kişilik, n≥2 ise oyun n kişili oyundur. Ayrıca sıfır toplamlı, sabit toplamlı olmayan ve sıfır toplamlı olmayan oyunlar olarak da oyunlar sınıflandırılır.
6. Tam (arı) Stratejiler: Herhangi bir tam strateji bir oyuncu için optimal için bu tam strateji diğer oyuncu için de optimaldir. Bu tam stratejiler maximin ve minimax kuralına göre ulaşılan değerleri veren stratejilerdir. Tam stratejiler, oyunun tepe noktasını belirler.
7. Karma Stratejiler: Oyunlarda genellikle daha etkili olan karma stratejiler kullanılır. Karma strateji, tam strateji takımındaki olasılık dağılımıyla tanımlanır.
8. Beklenen Değer: Belirsizlik altında karar verebilmek yani elverişli olan en iyi stratejiyi seçmede beklenen değer kavramı yararlıdır. Beklenen değer olayların olma olasılıkları ile olayın değerinin çarpımlarının toplamıdır.
9. Herhangi Bir Çözümün Tanımı: Herhangi bir oyunu çözümlerken, oyunun birkaç kez yinelenerek oynandığı düşünülür. İki kişili oyunda, A oyuncusu rakibi olan B oyuncusunun hangi stratejiyi oynayacağını düşünmeden kendisi için x gibi optimal strateji vektörünü elde etmeye çalışır, x vektörü A oyuncusuna oyundan maksimum beklenen kazancı sağlar. Buna karşılık B oyuncusu da A oyuncusunun beklenen kazancını en aza indirecek kendi strateji vektörü [y] yi araştırır. Eğer x* ve y*, A ve B oyuncularının optimal strateji vektörlerini gösterirse, A oyuncusunun beklenen değeri B.D.(x*,y*) olur ki, bu da oyunun değeridir. A ve B optimal şekilde oynarlarsa, B.D.(x*,y*) değeri yani (v), A oyuncusunun uzun dönem ortalama kazancı olur. Buradaki (v) oyunun değeridir.

1. n oyuncu sayısını göstermek üzere n≥2 dir. n=2 için “iki kişili oyun”, n>2 için “n kişili oyun” adı verilir. Oyuncu sayısı sonludur.
2. Her bir oyuncu rasyonel davranacaktır ve kendi çıkarını dikkate alarak karar verecektir.
3. Oyun sonucu; oyunu kazanma, kaybetme veya oyundan çekilme olarak belirlenir. Her bir sonuç (=outcome) veya ödeme; negatif, pozitif veya sıfır olmak üzere her oyuncunun diğerine ödemeleriyle belirlenir.
4. Tarafların seçenekleri belirlidir veya her bir oyuncunun davranışlar seti (=S1, S2, S3... gibi) rakibince bilinmektedir.
5. Her bir oyuncunun seçenek sayısı sonludur.

1. OYUN TEORİSİ İÇİN BAŞLICA ÖNERMELER

M satır ve n sütunu gösterirse (mxn) bir dikdörtgen oyunudur. Her dikdörtgenin bir oyun değeri vardır. Dikdörtgen oyunda herhangi bir oyuncunun her zaman optimal stratejisi vardır. Bu, şöyle ifadelendirilir:

B.D.(x*,y*)=v

1. A oyuncusunun her tam strateji vektörü xt için B.D.( xt, y*) ≤v dir. Bu şu demektir: Eğer B oyuncusu optimal stratejisini oynarsa, A oyuncusunun oynayacağı v değerinden daha fazla kazandırabilecek strateji yoktur.
2. B oyuncusunun her tam strateji vektörü yt için B.D.( x*, yt) ≥v dir.

Bir oyunda iki oyuncu varsa oyun iki kişili oyundur. İki kişili bir oyunda oyuncuların kazançları toplamı sıfırsa oyun, iki kişili sıfır toplamlıdır. Burada;

• Biri satır oyuncusu, diğeri sütun oyuncusu olarak adlandırılan iki oyuncu vardır. Satır oyuncusu yerine bizim taraf, sütün oyuncusu yerine de karşı taraf deyimlerine rastlanabilir.
• Satır oyuncusu için m, sütün oyuncusu n tane mümkün strateji vardır. Bu oyun kısaca mxn oyun olarak isimlendirilir.
• Satır oyuncusu stratejilerini, R1, R2, ..., Rm ile sütun oyuncusunun stratejilerini, C1, C2, ..., Cn ile gösterelim. Oyuncuların strateji seçimlerinin türlü bileşimlerinden sonuçlanan kazanç veya kayıpları bildiğimizi varsayalım. Bu tabloya, ödül, ödeme, kazanç veya kısaca “oyun matrisi” denir.

Satır oyuncusunun Ri, sütun oyuncusunun CJ gibi belirli bir stratejiyi kabul ettiklerini varsayalım. Oyun matrisi satır oyuncusuna göre düzenlenmiş ise aij satır oyuncusunun kazancını (sütun oyuncusunun kaybını) gösterir.

Örnek 1 : Aşağıdaki kazanç matrisini dikkate alarak, oyuncuların hangi stratejilerle oynayacağını belirleyiniz.

Her oyuncunun üçer stratejisi bulunduğundan oyun bir 3 x 3 oyunudur. İlk önce satır oyuncusuna bakılırsa; bu oyuncu R1 stratejisini seçerse, sütun oyuncusu C3 stratejisini seçerek kendi kaybını dolayısıyla rakibinin kazancını mümkün olan en düşük düzeyde düşer. Bu değer yukarıdaki matrise eklenen “satır en küçüğü” sütununda gösterildiği gibi 7’dir. Satır oyuncusunun ikinci stratejiyi seçmesi durumunda sütundaki oyuncu gene kendisi için en az (4) kayıp sağlayacak olan stratejiyi yani, üçüncü stratejiyi seçecektir. Sonuçta, satır oyuncusu için en iyi strateji, R1’dir.

1. TEPE NOKTASI KAVRAMI (TAM STRATEJİLER)

Oyunların en basiti tepe noktalı oyunudur. Yani satırında en küçük ve sütununda en büyük bir tek elamanı olan ödemeler matrisi düşünülmektedir. Bu durumda A ya göre oyunun değeri tepe noktası elemanı ve B ye göreyse tepe noktası elemanın negatif işaretlisidir.

Örnek 2 : A ya göre ödemeler matrisi aşağıda verilmektedir. Her bir oyuncu için en iyi seçeneği, A ve B ye göre oyun değerini bulunuz.

				B
							Satırların
		I	II	III	IV	V	Min. Elemanı
	I	9	3	1	8	0	0
A	II	6	5	4	8	7	4
	III	2	4	3	3	8	2
	IV	5	6	2	2	1	1
	Sütunların
	Max. Elemanı	9	6	4	8	8

 

Verilen A ya göre ödemeler matrisinde her bir satırın en küçük elemanı matrisin sol tarafına ve B ye göreyse ödemeler matrisi kayıp değerleri göstermesi nedeniyle her bir sütunun en büyük elemanı matrisin altına yazılır. Bu düşünce A yönünden maximin yani kötümserlik kriteri ve B yönünden kayıp söz konusu olduğu için minimax (=maliyet tipli karar matrisinde kötümserlik kriteri) olarak belirlenir. A için oyun değeri 4 ve B için oyun değeri 4 olarak bulunması nedeniyle her iki oyuncunun oyundan beklediği değerler (birinin kazancı diğerinin kaybı olarak düşünüldüğü için) birbirini karşılamaktadır ve oyunun bir tepe noktası vardır. A nın seçeneği II. strateji, B nin seçeneği de III. stratejidir ve tam stratejileridir. Oyunun tepe noktası olması dolayısıyla da oyunun değeri 4 dür.

2. TEPE NOKTASIZ OYUNLAR VE KARMA STRATEJİLER

Bir m x n oyununun tepe noktası yoksa, özellikle m ve n’nin büyük değerleri için oyunun çözümü zor olabilir. Genel olarak bir oyunun tepe noktası yoksa oyunu çözmeden önce mümkünse m ve ne değerleri küçültülmesi yani, bazı stratejilerin devre dışı bırakılmaları uygun olur. Bu işlem ancak bazı özel stratejilerin belirlenmesiyle gerçekleşir. Boyut küçültmede kullanılabilecek iki çeşit strateji vardır: Eş stratejiler ve Üstünlük stratejileri

1. Eş Stratejiler

Örnek 3 : Kazanç matrisi aşağıda gösterilen oyunun eş stratejilerini belirleyiniz.

Satır		Sütun Oyuncusu
Oyuncusu		Stratejisi
Stratejisi	C1	C2	C3	C4
R1	1	2	3	1
R2	3	6	1	3
R3	0	5	4	0
R4	1	2	3	1

C1 ve C4 stratejileri kazançların, bire bir olmak üzere eşit oldukları görülebilir. Bunlardan biri diğerine tercih edilemez. Bu yüzden birini, C4 veya C1’i göz ardı etmek mümkündür. Bu yolla bu oyunun boyutu 4 x 4’den 4 x 3’e indirgenmiş olur. Benzer şekilde R1 ve R4 stratejileri de eş stratejiler olduklarından bir dışta bırakılabilir. Böylece oyun 3 x 3 boyutuna indirgenmiş olur.

Örnek 4 : Kazanç matrisi aşağıda gösterilen oyunun tepe noktasını belirleyerek oyuncuların en iyi stratejilerini bulunuz.

Satır		Sütun Oyuncusu			Satır
Oyuncusu		Stratejisi			En
Stratejisi	C1	C2	C3	C4	Küçüğü
R1	10	10	8	17	8
R2	17	-13	26	23	-13
R3	-30	30	25	13	-30
R4	24	32	14	25	14
Sütun
En Büyüğü	24	32	26	25	14 ≠ 24

Matrisin son gözesinde gösterildiği gibi ( 14 ≠ 24 ) oyunun alt ve üst değerleri birbirlerine eşit olmadıklarından oyunun tepe noktası yoktur. Bu durumda maximin ve minimax stratejilerden dolayısıyla, sade stratejilerden söz edilemez.

 

2. Üstünlük Stratejileri

Tarafların seçenekleri zayıf ve üstün seçenekler olarak ikiye ayırma olanağı bazı oyunlarda söz konusudur. Sıfır toplamlı-iki kişili oyunlarda tepe noktası bulunmadığı zaman ikinci bir kontrol bir satır veya sütun elemanlarının diğer satır veya sütun elemanlarından büyük veya küçük olmasına bakmaktır. Satırlar için bu tarama işlemi, A oyuncusunun kazançlarını gösterdiğine göre, bir satırdaki her bir elemanın diğer bir satırdan daha büyük olması, o satırın ilk olarak benimsenileceğini gösterir ve üstün seçenektir. Üstün seçeneğin satır elemanlarının karşılaştırıldığı satır elemanları hemen tercih edilen kazanç olmadığı için de zayıf seçenek adı verilir. Sütunlar için de benzer karşılaştırma söz konusudur. O halse zayıf seçenek, tarafların hiç bir zaman benimsemeyecekleri seçeneklerin ödemeler matrisinden çıkartılmasıdır. Bu işlemle ödemeler matrisi daha küçük boyutlara indirgenmiş olur. Üstün seçenekler ilkesi ile ödemeler matrisinin zayıf seçenekleri elimine edilmiş olur.

Örnek 5 : A ve B firmalarının reklam kampanyası planlarına göre verilmiş olan ödemeler matrisi, firmaların Pazar paylarını göstermekte olduğuna göre firmaların seçeneklerini belirleyiniz.

1. ---

   reklam yapmamak

2. ---

   orta çapta reklam yapmak

3. ---

   büyük çapta reklam yapmak

Satırlar taranarak minumum elemanlar, sütunlar taranarak maximum elemanlar ödemeler matrisinde gösterilmiştir. Satırlarım maximin elemanı 60 ve sütunların minimax elemanı olan 70 birbirine eşit olmadığından oyunda tepe noktası yoktur. Yani A firması 3 nolu seçeneğini ve B firması 2 nolu seçeneğini benimsemesi halinde bir denge olamaz. Örneğin A, 2 nolu seçeneğine kayarsa, B 3 nolu seçeneğini ileri sürebilir ve oyuna çözüm bulunamadan bu değişim devam eder.

Üstün seçenekler ilkesini uygulama şöyle olacaktır: B firması 1 nolu seçeneğini hiçbir zaman tercih etmeyecektir. Zira karşılaştırılırsa, birinci sütun elemanlarının büyük olduğu görülür. Dolayısıyla B her zaman daha büyük kayıpları istemez ve birinci seçeneğini kullanmaz. Benzer bir taramayla A içindeki birinci seçenek elimine edilir. Böylece çözüm diğer iki seçenek arasında bulunacaktır. Bu işlem aşağıdaki gibi gösterilerek elimine edilen seçenekler belirlenmiş olur.

B

60 50 40

A 70 70 50

80 60 75

Elimine edilen seçeneklerden sonra geri kalan ödemeler matrisi tekrar yazılırsa;

B oyuncusu 2 nolu seçeneğini Y2, 3 nolu seçeneğini Y3 kez oynayacağına göre A oyuncusunun beklenen kazancı;

E1 70 Y2 + 50 (1 - Y2 ) = v

E2 60 Y2 + 75 (1 - Y2 ) = v

olur. Y1 + Y2 + Y3= 1 olduğundan, Y1 = 0 için Y2 + Y3= 1 ve Y3 = 1 – Y2 sonucu E1 de yerine konmuştur. Denklem sistemi çözülerek Y2 = 5 / 7 , Y3 = 2 / 7 ,

v = 450 / 7 bulunur.

50 X2 + 75 ( 1 – X2) = v

70 X2 + 60 ( 1 - X2 ) = v

denklem sisteminden X2 = 3 / 7 , X3 = 4 / 7 , v = 450 / 7 bulunur.

Çözüm>>> X ( 0,3 / 7 , 4 / 7 ) ; Y ( 0,5 / 7 , 2 / 7 ) ; v = 450 / 7 olarak yazılır.

7.GRAFİK ÇÖZÜM TEKNİĞİ

Üstünlük stratejisi ile oyunlar m x 2 ve 2 x n boyuta indirgenirse bu oyunlar grafik yöntemiyle çözülebilir.

Örnek 6 : A ve B oyuncuları arasında oynanan (2x4) boyutlu oyunun matrisi verilmiştir. Buna göre oyunu grafik yöntemine göre çözünüz.

Oyun matrisinin tepe noktası yoktur. A oyuncusunun A1 stratejisini oynama olasılığına x dersek, A2 stratejisini oynama olasılığı da ( 1 – x ) olur. B oyuncusunun A oyuncusuna yapacağı beklenen ödemeleri veya beklenen değerleri, B’nin tam stratejilerine göre şöyle olacaktır:

B1 9x – 2 (1-x) = 11x - 2

B2 -3x + 3 (1-x) = 3 – 6x

B3 -4x + 5 (1-x) = 5 – 9x

B4 6x – 1 (1-x) = 7x – 1

Oyunları çözmek için uygun teknikleri geliştirmede kullanılacak iki temel önermeden ikincisine göre, tablonun sağ tarafındaki denklemlerin her biri oyun değeri (v) ye eşit veya ondan daha büyük olmalıdır.

Maksimum Z = v

11x – 2 ≥ v

3– 6x ≥ v

5– 9x ≥ v

7x – 1 ≥ v

ve

0 ≤ x ≤ 1

Dikkat edilirse v için negatif olmama koşulu yoktur. Elimizde x ve v gibi iki karar değişkeni bulunduğundan, problemi grafik yöntemiyle çözebiliriz. Alışılmış olarak v dikey eksende, x de yatay eksende gösterilir. Problemdeki son kısıtlayıcı yüzünden x sadece 0 ile 1 aralığı içinde yer alır. Grafik çözüm tekniğine göre x ve v değerlerini elde edelim:

• 11x – 2 = v denkleminde,

x = 0 için v = -2

x = 1 için v = 9

v = 0 için x = 2 / 11 dir.

• 3– 6x = v denkleminde,

x = 0 için v = 3

x = 1 için v = -3

v = 0 için x = 1 / 2 dir.

• 5– 9x = v denkleminde,

x = 0 için v = 5

x = 1 için v = -4

v = 0 için x = 5 / 9 dur.

• 7x – 1 = v denkleminde,

x = 0 için v = -1

x = 1 için v = 6

v = 0 için x = 1 / 7

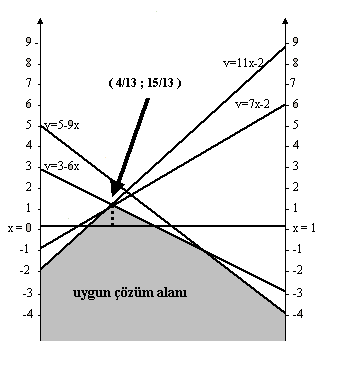
Şimdi bu değerleri yerlerine koyarak grafiğimizi çizelim.

Uygun çözüm alanındaki maksimum kazancı verecek x in optimal değerini bulmak için;

v = 3 – 6x

v = 7x – 1 denklemlerinden yararlanılır.

3 – 6x = 7x – 1 13x = 4 v = 15 / 13 dür.

Şekildeki taralı alanın en yüksek noktası (4/13 , 15/13) dir. Böylece oyunun değeri v= 15/13, x’in optimal değeri de x* = 4/13 dir. A oyuncusunun optimal strateji vektörü,

x*=(4/13 , 9/13) olur.

Grafikte de görüldüğü gibi, maksimum yani en yüksek noktadan iki doğru geçer ki, bunlar da B oyuncusunun B2 tam stratejisine, v = 7x – 1 doğrusu da B4 stratejisine karşılıktır. Bu demektir ki, B oyuncusunun optimal stratejisi sadece B2 ve B4 stratejilerinin karması olacaktır. Geriye kalan B1 ve B3 stratejileri hiçbir zaman oynanmayacaktır. 2xn oyunlarında bir genelleme için şunu söyleyebiliriz. Maksimum noktadan geçmeyen doğruların stratejileri hiçbir zaman oynanmamalıdır. Böylece örneğimizde y1 = y3 = 0 olur. Eğer A oyuncusu A1 stratejisini oynarsa A ya beklenen ödeme; 9y1 - 3y2 - 4y3 + 6y4 olur. Eğer A oyuncusu A2 stratejisini oynarsa A ya beklenen ödeme -2y1 + 3y2 + 5y3 – y4 olur. Aynı zamanda bu denklemler oyunun değerine eşit olmalıdır. Öyleyse,

9y1 - 3y2 - 4y3 + 6y4 = v

-2y1 + 3y2 + 5y3 – y4 = v

ve

y1 = y3 = 0 olduğundan

-3y2+ 6y4 = 15 / 13

-3y2 – y4 = 15 / 13

Bu denklemim çözümü de bize

y4 = 6 / 13 y2 = 7 / 13 verir.

Aynı zamanda bu değerler B oyuncusunun optimal strateji vektörünün değerleri olur. Buna göre B oyuncusunun optimal strateji vektörü:

y * = 0 , 7 / 13 , 0 , 6 / 13 dir.

Bugünün dünyasında, çok hızlı değişim ve gelişim içerisindedir. Böyle bir ortamda işletmeler ayakta kalabilmeleri, yapacakları iç ve dış işletme analizlerine ve bu analizler ışığında alınacak kararlara bağlıdır.

Karar alma tekniklerinden biri de oyun teorisidir. Oyun teorisini tarihsel gelişimi irdelendiğinde, oyunların şans kuramı 17. Yüzyılda ortaya atılmış ve olasılık kuramı adı verilen matematik dalının gelişmesinde kaynak olduğu görülür. Çıkarları çatışan tarafların akılcı davranış kurallarının belirlenmesi olan oyun teorisi, bu tür karar ortamlarını açıklayan matematiksel bir yaklaşımdır.

• Cinemre, Nalan; Yöneylem Araştırması, Beta Basım Yayım Dağıtım A.Ş., İstanbul, 1997.

• Friedman, James W.; Game Theory With Applications To Economics, 2^nd ed., Oxford University Press, New York, 1990.

• Fudenberg, Drew and Jean Tirole; Game Theory, The MIT Press, Massachusetts, 1998.

• Halaç, Osman; Kantitatif Karar Verme Teknikleri (Yöneylem Araştırması), 4.b., Alfa Basım Yayım Dağıtım, İstanbul, 1995.

• Hodgetts, Richard M.; Yönetim, 2.b., çev. Canan Çetin, Esin (Can) Mutlu, Beta, İstanbul, 1999.

• Öztürk, Ahmet; Yöneylem Araştırması, 5.b., Ekin Kitapevi Yayınları, Bursa, 1997.

• Romp, Graham; Game Theory-Introduction and Applications, Oxford University Press, Great Britain, 1997.